provides an excellent way to represent subtraction.
Let’s start with addition as represented on a number line.
Let’s take the addition problem 7 + 3 = 10.
To show this on a number line, we first start from zero and count 7
units to the right. The distance from zero to that point is the number
7.
Fig. 1

Because a number is a distance, we’ll represent numbers using arrows rather than just points for now.
So now we have seven, how do we add 3 to it?
Fig. 2
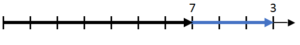
We start at the point for 7, and continue counting to the right for 3 more units, as shown above. I like to refer to this as “connect and count.” Here, “connect” is a shorthand way of saying that you start counting the second addend from the end of the first addend. And, of course, because these are positive numbers, you count to the right after you “connect.”
To find the result of addition, the sum, we start at zero and count the distance to the end of the second addend as shown below.
Fig. 3

To summarize, to add numbers on a number line:
1. We, start at zero and count the first addend to the right (Fig. 1)
2. We start at the end of the first addend (“connect”) and count the second addend to the right (Fig. 2)
3. We start at zero and count the distance to the end of the second addend to find the sum. (Fig. 3)
Now let’s look at how we represent subtraction, using the definition of subtraction as “finding the missing addend.” To do that, we use the addition shown on the number line, but we remove the second addend.

This is a representation of a “missing addend.” As shown in Figure 3, we know that one addend is seven, and we know that the sum is 10. In this case, what we don’t know is the second addend, which we know from the earlier addition problem is the distance from the end of the first addend to the end of the sum.
To find this distance, which is the difference, we first “connect,” that is, we start counting at the end of the first addend. But this, time, we don’t know how many units we count, but we do know when to stop counting. We stop when we get to the sum, which is 10. When we count, we keep track of how many units we count in order to reach the sum.

That number of units is the missing addend. It’s also the distance from the end of the first addend to the end of the sum (which is exactly what it was in the addition situation).
To summarize, to subtract numbers on a number line:
1. We, start at zero and count the first addend to the right
2. We start at zero and count the sum to the right
3. We start at the end of the first addend and count to the end of the sum
In both addition and subtraction, we start by counting the known addend, starting from zero.
Also, in both addition and subtraction, we “connect and count.” That is, we start counting at the end of the first addend – the known addend. The difference in addition and subtraction is this:
• With addition, we know how many units we count (addend), but we don’t know where we will end up (sum)
• With subtraction, we know where we will end up (sum), but we don’t know how many units we count.
This leads to an important general statement of what subtraction is on a number line:
Subtraction is finding the difference, which is the distance between two
points on the number line.
This understanding of what subtraction is, is simple and intuitive, but in spite of that, it’s exactly what subtraction is.
But, you may be thinking…whoa, wait a minute. That’s not what subtraction is. Subtraction requires counting back from the sum.
Turns out, (in my opinion) that’s the erroneous conception of subtraction that has led us astray since the beginning of public education in this country.
That erroneous conception of subtraction as “counting back” is highly correlated with the erroneous interpretation of subtraction as “take away,” as discussed in two prior posts:
Subtraction Does Not Mean “Take Away” and What is Subtraction?.”
The “take away” interpretation of subtraction is usually represented on a number line as “counting back,” like this.

One reason for this is the notion that subtraction “undoes” addition, which is often offered as an informal statement of what it means to say that “subtraction is the inverse of addition.” Intuitively, when representing the notion of “undoing”, it makes sense to “count back” from
the sum to find the other addend. For that reason, I have a problem with this informal notion of “undoing”. In my opinion, it hurts more than it helps. However, one could still think of subtraction as “undoing”. The key step in addition is counting the second addend from the end of the first. One could think of subtraction as “undoing” where the undoing is “removing the arrow” that represents the second addend.
Another reason for the popularity of the “counting back” interpretation on a number line is that it models the process of “counting back” through the counting sequence (on one’s fingers to begin with) as a way of determining the difference. This strategy is used by some children before the basic facts are committed to memory.
Even though counting back (even on one’s fingers) is known to be very difficult for students, this way of thinking of subtraction still seems to have intuitive appeal. Finally, by counting back to show the known addend, you end up at a point on the number line that allows you to simply “read” the value of the difference from the numbers labeling the units on the line. The reason for this is that the unknown addend in this representation is the distance from zero to the ending point of the count, as illustrated below.

While this is a “convenience” it is not a requirement of using the number line. For example, when using a number line, we tend to forget that we can count a number by starting from any point on the line. That’s as legitimate as counting a number starting at zero.
In fact, that’s exactly what we do when we “connect and count” to show addition. The first addend is counted from zero, but the second addend is counted from the end of the first addend, not zero.
That means we haven’t done anything that is mathematically incorrect by counting the difference by starting at the end of the first addend.
This interpretation of subtraction on a number line as finding a missing addend will almost certainly seem strange to most people. But it’s a very easy way to illustrate the concept of subtraction, and it’s mathematically correct.
When I came upon this approach, it was the culmination of many stumbling attempts to avoid the problems associated with explaining why subtracting a negative number is the same as adding a positive number. What I found in the process was that the missing addend approach not only solves that problem, but has other powerful benefits as well.
